Поляризация волны – Поляризация электромагнитных волн

Содержание

Поляризация электромагнитных волн | Наука

Поляризация электромагнитных волн (ПЭВ) — одно из фундаментальных свойств оптического излучения (света), состоящее в искажении различных направлений в плоскости, перпендикулярной световому лучу (направлению распространения световой волны).^[1]

ПЭВ — явление направленного колебания векторов напряженности электрического поля E или напряженности магнитного поля H.

Когерентное электромагнитное излучение может иметь:

Эллипс поляризации

Линейную поляризацию — в направлении, перпендикулярном направлению распространения волны;
Круговую поляризацию — правую либо левую, в зависимости от направления вращения вектора индукции;
Эллиптическую поляризацию — случай, промежуточный между круговой и линейными поляризациями.

Некогерентное излучение может не быть поляризованным, может быть полностью или частично поляризованным любым из указанных способов. В таком случае понятие поляризации понимается статистически.

При теоретическом рассмотрении поляризации волна полагается распространяющейся горизонтально. В этом случае можно рассматривать вертикальную и горизонтальную линейные поляризациии волны.

Для понимания явления поляризации света имело её проявление в эффекте интерференции света. Именно тот факт, что когда два световых луча, линейно поляризованных под прямым углом друг к другу, при простейшей постановке опыта не интерферируют, явился решающим доказательством поперечности световых волн (Френель, Араго, Т. Юнг, 1816—19). Поляризация света нашла естественное объяснение в электромагнитной теории света Дж. К. Максвелла (1865—73).

Поперечность световых волн (как и любых др. электромагнитных волн) выражается в том, что колеблющиеся в них векторы напряжённости электрического поля интерференции Е и напряжённости магнитного поля Н перпендикулярны направлению распространения волны. Е и Н выделяют (отсюда указанное выше неравноправие) определённые направления в пространстве, занятом волной. При этом Е и Н почти всегда взаимно перпендикулярны, поэтому для полного описания состояния поляризация света требуется знать поведение лишь одного из них. Обычно для этой цели выбирают вектор Е.

Круговая поляризацияПравить

Круговая поляризация — состояние распространяющейся электромагнитной волны (например, световой), при котором концы её электрического и магнитного векторов Е и Н в каждой точке пространства, где проходит волна, описывают окружности в плоскости, перпендикулярной направлению распространения волны.

В России и США используются спутниковы станции, оснащённые вращающимися антенами с круговой поляризацией. В Европе — навигационные телевизионные станции оснащены прямолинеёной поляпизацией. Исторически так сложилось, что раньше СССР использовал для ТВ вещания спутники серии «Молния», находящиеся на высокоэлептических орбитах. Для приема сигнала и слежения за спутниками использовались станции, оснащенные весьма большими антеннами и дорогим высокочувствительным оборудованием Орбита 1-3 (такая станция долго стояла в Хабаровске). Это было связано с тем, что спутники постоянно двигались, и в случае использования круговой поляризации не требовалось корректировать поляризацию в зависимости от положения спутника. В случае применения линейной поляризации, то ее пришлось бы постоянно вращать. Например, в США за стандарт аналогично принята круговая поляризация (например, Интелсаты везде применяют круговую поляризацию).

Использование линейной поляризации в европеёских странах вызвано тем, что всё спутниковое вещание в Европе началось в конце 80-х годов. Для него были использованы спутники, находящиеся на стабильных геостационарных орбитах и для вещания в Ku-band в Европе была принята линейная поляризация.

Не исключено, что в ближайшее время при вещании на Россию в C-band не будет линейной поляризации, т.к. в России для спутникового вещания в качестве стандарта принята круговая поляризация.

Электромагнитная волна может быть разложена (как теоретически, так и практически) на две поляризованные составляющие, например поляризованные вертикально и горизонтально. Возможны другие разложения, например по иной паре взаимно перпендикулярных направлений, или же на две составляющие, имеющие левую и правую круговую поляризацию. При попытке разложить линейно поляризованную волну по круговым поляризациям (или наоборот) возникнут две составляющие половинной интенсивности.

Как с квантовой, так и с классической точки зрения, поляризация может быть описана двумерным комплексным вектором (вектором Джонса). Поляризация фотона является одной из реализаций q-бита.

Свет солнца, являющийся тепловым излучением, не имеет поляризации, однако рассеянный свет неба приобретает частичную линейную поляризацию. Поляризация света меняется также при отражении. На этих фактах основаны применения поляризующих фильтров в фотографии и т. д.

Линейную поляризацию имеет обычно излучение антенн.

По изменению поляризации света при отражении от поверхности можно судить о структуре поверхности, оптических постоянных, толщине образца.

Если рассеянный свет поляризовать, то, используя поляризационный фильтр с иной поляризацией, можно ограничивать прохождение света. Интенсивность света прошедшего через поляризаторы подчиняется закону Малюса. На этом принципе работают жидкокристаллические экраны.

История открытия Править

Открытию поляризованных световых волн предшествовали работы многих учёных. В 1669 г. датский учёный Эразм Бартолин сообщил о своих опытах с кристаллами известкового шпата (CaCO₃), чаще всего имеющими форму правильного ромбоэдра, которые привозили возвращающиеся из Исландии моряки. Он с удивлением обнаружил, что луч света при прохождении сквозь кристалл расщепляется на два луча (называемых теперь обыкновенным и необыкновенным). Бартолин провёл тщательные исследования обнаруженного им явления двойного лучепреломления, однако объяснения ему дать не смог.

Через двадцать лет после опытов Э. Бартолина его открытие привлекло внимание нидерландского учёного Христиана Гюйгенса. Он сам начал исследовать свойства кристаллов исландского шпата и дал объяснение явлению двойного лучепреломления на основе своей волновой теории света. При этом он ввёл важное понятие оптической оси кристалла, при вращении вокруг которой отсутствует анизотропия свойств кристалла, то есть их зависимость от направления (конечно, такой осью обладают далеко не все кристаллы).
В своих опытах Гюйгенс пошёл дальше Бартолина, пропуская оба луча, вышедшие из кристалла исландского шпата, сквозь второй такой же кристалл. Оказалось, что если оптические оси обоих кристаллов параллельны, то дальнейшего разложения этих лучей уже не происходит. Если же второй ромбоэдр повернуть на 180 градусов вокруг направления распространения обыкновенного луча, то при прохождении через второй кристалл необыкновенный луч претерпевает сдвиг в направлении, противоположном сдвигу в первом кристалле, и из такой системы оба луча выйдут соединёнными в один пучок. Выяснилось также, что в зависимости от величины угла между оптическими осями кристаллов изменяется интенсивность обыкновенного и необыкновенного лучей.

Эти исследования вплотную подвели Гюйгенса к открытию явления поляризации света, однако решающего шага он сделать не смог, поскольку световые волны в его теории предполагались продольными. Для объяснения опытов Х. Гюйгенса И. Ньютон, придерживавшийся корпускулярной теории света, выдвинул идею об отсутствии осевой симметрии светового луча и этим сделал важный шаг к пониманию поляризации света.

В 1808 г. французский физик Этьен Луи Малюс, глядя сквозь кусок исландского шпата на блестевшие в лучах заходящего солнца окна Люксембургского дворца в Париже, к своему удивлению заметил, что при определённом положении кристалла было видно только одно изображение. На основании этого и других опытов и опираясь на корпускулярную теорию света Ньютона, он предположил, что корпускулы в солнечном свете ориентированы беспорядочно, но после отражения от какой-либо поверхности или прохождения сквозь анизотропный кристалл они приобретают определённую ориентацию. Такой «упорядоченный» свет он назвал поляризованным.

Параметры Стокса Править

Изображение поляризации языком параметров Стокса на сфере Пуанкаре

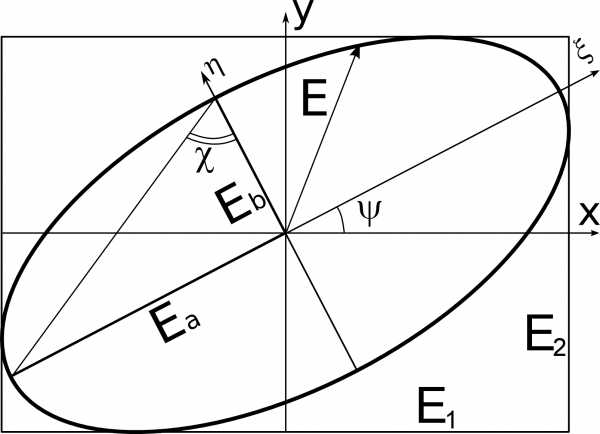
В общем случае плоская монохроматическая волна имеет правую или левую эллиптическую поляризацию. Полная характеристика эллипса даётся тремя параметрами, например, полудлинами сторон прямоугольника, в который вписан эллипс поляризации $ A_1 $, $ A_2 $ и разностью фаз $ \phi $, либо полуосями эллипса $ a $, $ b $ и углом $ \psi $ между осью $ x $ и большой осью эллипса. Удобно описывать эллиптически поляризованную волну на основе параметров Стокса:

$ S_0=A^2_1+A^2_2 $, $ S_1=A^2_1-A^2_2 $,

$ ~S_2=2A_1 A_2 \cos \phi $, $ ~S_2=2A_1 A_2 \sin \phi $.

Независимыми являются только три из них, ибо справедливо тождество:

$ S^2_0=S^2_1+S^2_2+S^2_3 $.

Если ввести вспомогательный угол $ \chi $ , определяемый выражением $ \chi=\pm a/b $ (знак $ ~+ $ соответствует правой, а $ ~- $ — левой поляризации), то можно получить следующие выражения для параметров Стокса:

$ ~S_1=S_0 \cos (2\chi) \cos (2\psi) $,

$ ~S_2=S_0 \cos (2\chi) \sin (2\psi) $,

$ ~S_3=S_0 \sin (2\chi) $.

На основе этих формул можно характеризовать поляризацию световой волны наглядным геометрическим способом. При этом параметры Стокса $ ~S_1 $, $ ~S_2 $, $ ~S_3 $ интерпретируются, как декартовы координаты точки, лежащей на поверхности сферы радиуса $ ~S_0 $. Углы $ ~2\chi $ и $ ~2\psi $ имеют смысл сферических угловых координат этой точки. Такое геометрическое представление предложил Пуанкаре, поэтому эта сфера называется сферой Пуанкаре.

Наряду с $ ~S_1 $, $ ~S_2 $, $ ~S_3 $ используют также нормированные параметры Стокса $ ~s_1=S_1/S_0 $, $ ~s_2=S_2/S_0 $, $ ~s_3=S_3/S_0 $. Для поляризованного света $ ~s^2_1+s^2_2+s^2_3=1 $.

Использование явления поляризации светаПравить

Особенности взаимодействия поляризованного света с веществом позволили найти его широкое применение в научных исследованиях, в определении структуры твёрдых тел, строения биологических объектов (см., например, поляризационная микроскопия), состояний элементарных излучателей и их отдельных центров, ответственных за квантовые переходы, для получения информации о сильно удаленных (в частности, астрофизических) объектах. Вообще, поляризация света как существенно анизотропное свойство излучения, позволяет изучать все виды анизотропии вещества — поведение газообразных, жидких и твёрдых тел в полях анизотропных возмущений (механических, звуковых, электрических, световых), в структуре — в подавляющем большинстве — оптически анизотропных материалов, в технике (например, в машиностроении) — упругие напряжения в конструкциях (например, поляризационно-оптический метод исследования напряжений) и т.д.

Взаимодействие поляризованного света с веществом может приводить к оптической ориентации или к настройке генерации мощного поляризованного излучения в лазерах и др. С другой стороны, исследование деполяризации света при фотолюминесценции дает сведения о взаимодействии поглощающих и излучающих центров в частицах вещества, при рассеянии света — ценные данные о структуре и свойствах рассеивающих молекул или иных частиц, в других случаях — о протекании фазовых переходов и т.д. (См. также Флюоресцентный наноскоп).

Поляризация света широко используется в технике, например при необходимости плавной регулировки интенсивности светового пучка (см. Малюса закон), для усиления контраста и устранения световых бликов в фотографии, при создании светофильтров (например, поляризационных), модуляторов излучения (см. Модуляция света), служащих одними из основных элементов систем оптической локации и оптической связи для изучения протекания реакций, строения молекул, определения концентраций растворов (см. Поляриметрия, Сахариметрия) и др.

Поляризация светового излучения играет заметную роль в живой природе. Многие живые существа способны чувствовать поляризацию света, а некоторые насекомые (пчёлы, муравьи) ориентируются в пространстве по поляризованному (в результате рассеяния в атмосфере) свечению голубого неба. При определенных условиях к Поляризация света становится чувствительным и человеческий глаз (т. н. явление Хайдингера). ^[2]

Ахманов С. А., Никитин С. Ю. — Физическая оптика, 2 издание, M. — 2004.
Борн М., Вольф Э. — Основы оптики, 2 издание, исправленное, пер. с англ.,М. — 1973

↑ http://bse.sci-lib.com/article091314.html
↑ http://www.oval.ru/enc/56254.html

ru.science.wikia.com

Поляризация волн | Наука | FANDOM powered by Wikia

Поляриза́ция волн — явление нарушения симметрии распределения возмущений в поперечной волне (например, напряжённостей электрического и магнитного полей в электромагнитных волнах) относительно направления её распространения. В продольной волне поляризация возникнуть не может, так как возмущения в этом типе волн всегда совпадают с направлением распространения.^[1]

Поперечная волна характеризуется двумя направлениями: волновым вектором и вектором амплитуды, всегда перпендикулярным к волновому вектору. Так что в трёхмерном пространстве имеется ещё одна степень свободы — вращение вокруг волнового вектора.

Причиной возникновения поляризации волн может быть:

несимметричная генерация волн в источнике возмущения;
анизотропность среды распространения волн;
преломление и отражение на границе двух сред.

Основными являются два вида поляризации:

линейная — колебания возмущения происходит в какой-то одной плоскости. В таком случае говорят о «плоско-поляризованной волне»;
круговая — конец вектора амплитуды описывает окружность в плоскости колебаний. В зависимости от направления вращения вектора может быть правой или левой.

На основе этих двух или только круговой можно сформировать и другие, более сложные виды поляризации. Например, эллиптическая.

Зависимость мгновенных потенциалов при круговой поляризации

Практическое значение Править

Скорость распространения волны может зависеть от её поляризованности.

Две волны, линейно поляризованные под прямым углом друг к другу, не интерферируют.

Чаще всего это явление используется для создания различных оптических эффектов, а также в 3D-кинематографе (технология IMAX), где поляризация используется для разделения изображений, предназначенных правому и левому глазу.

Круговая поляризация применяется в антеннах космических линий связи, так как для приёма сигнала не важно положение плоскости поляризации передающей и приёмной антенн. То есть вращение космического аппарата не повлияет на возможность связи с ним. В наземных линиях используют антенны линейной поляризации — всегда можно выбрать заранее — горизонтально, или вертикально располагать плоскость поляризации антенн. Антенну круговой поляризации выполнить сложнее, чем антенну линейной поляризации. Вообще, круговая поляризация — вещь теоретическая. На практике говорят об антеннах эллиптической поляризации — с левым или правым направлением вращения.

Круговая поляризация света используется также в 3D-кинематографе, в технологии RealD 3D. Эта технология подобна IMAX с той разницей, что круговая поляризация вместо линейной позволяет сохранять стереоэффект и избегать двоения изображения при небольших боковых наклонах головы.

Поляризация частиц Править

Аналогичный эффект наблюдается при квантовомеханическом рассмотрении пучка частиц, обладающих спином. Состояние отдельной частицы в этом случае, вообще говоря, не является чистым и должно описываться соответствующей матрицей плотности. Для частицы со спином ½ (скажем, электрона) это эрмитова матрица 2×2 $ \rho^a_b $ со следом 1:

$ \!\rho_{ab} = \rho^\dagger_{ab} = \bar \rho_{ba} $

$ \mathrm{tr}\, \rho^a_b = 1 $

В общем случае она имеет вид

$ \rho^a_b = {1\over 2}(\delta^a_b + 2 \hat{\mathbf{\sigma}^a_b} \bar{\mathbf{s}}) $

Здесь $ \hat{\mathbf{\sigma}} = (\sigma_x,\sigma_y,\sigma_z) $ — вектор, составленный из матриц Паули, а $ \bar{\mathbf{s}} $ — вектор среднего спина частицы. Величина

$ \rho = 2 |\bar{\mathbf{s}}| = 2 \sqrt{s_x^2 + s_y^2 + s_z^2} $

называется степенью поляризации частицы. Это вещественное число $ 0<\rho<1. $ Значение $ \rho =1 $ соответствует полностью поляризованному пучку частиц, при этом

$ \rho^a_b = \psi^a \otimes \psi^\dagger_b $

где $ \psi $ — вектор состояния частицы. Фактически, полностью поляризованные частицы можно полностью описать вектором состояния.

Физика. Большой энциклопедический словарь/Гл. ред. А. М. Прохоров. — 4-е изд. — М.: Большая Российская энциклопедия, 1999. — С. 87. ISBN 5-85270-306-0 (БРЭ)

↑ http://bse.sci-lib.com/article091310.html

ru.science.wikia.com

Поляризация электромагнитных волн

При рассмотрении плоской волны в однородной изотропной среде было показано, что она является поперечной, т.е. векторы иперпендикулярны направлению распространения (оси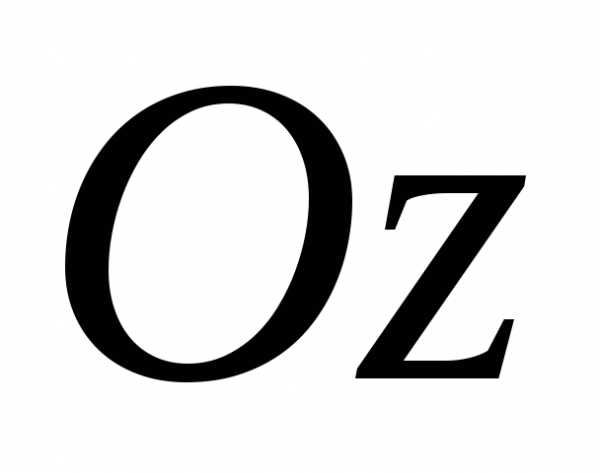). В целях упрощения полагалось, что векторориентирован вдоль оси, и было установлено, что в этом случае векторориентирован по оси(рисунок Рисунок 50 ).

−Простейший случай линейно поляризованной волны

Однако следует иметь в виду, что ориентация векторов иотносительно координатных осей зависит от источника, создающего волну. В общем случае направления векторов могут отличаться от направления координатных осей, а значит, каждый из векторов поля может иметь составляющие по обеим координатным осям, причем начальные фазы составляющих могут отличаться. Это приводит к тому, что положение векторав пространстве будет отличаться от простейшего случая, когда этот вектор всегда колеблется в плоскости.

Поляризация электромагнитной волы − ориентация в пространстве вектора напряженности электрического поля .

Различают три вида поляризации: линейную, круговую и эллиптическую. Как будет показано, все эти три вида являются частными случаями общего эллиптического представления.

Линейная поляризация

Простейшим случаем является линейная поляризация. Если рассмотреть выражение для вектора :

то окажется, что половину периода направление вектора совпадает с положительным направлением оси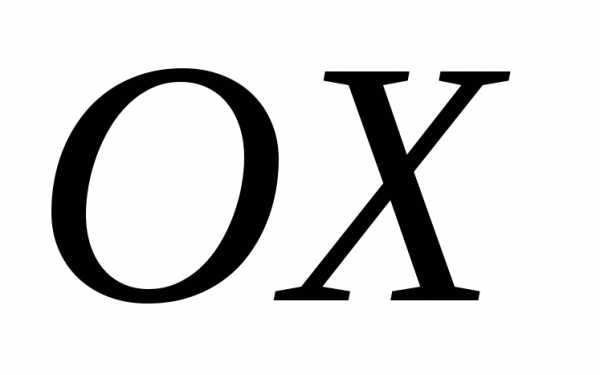, а вторую половину − противоположно ему (рисунок Рисунок 51 ). Таким образом, в фиксированной точке пространстваконец векторас течением времени перемещается вдоль отрезка прямой линии, а величина вектора изменяется в интервале. Волны, имеющие такой характер ориентации вектора, называются линейно поляризованными. Плоскость, проходящую через направление распространение волны и вектор, называют плоскостью поляризации. В рассматриваемом примере плоскостью поляризации является плоскость.

−Электромагнитная волна с линейной поляризацией

Линейная поляризация исключительно часто применяется в антенной технике. Так, все местное (не спутниковое) теле- и радиовещание производится на радиоволнах линейной поляризации. Положение плоскости поляризации полностью определяется ориентацией приемных и передающих антенн. Так как плоскостью линейной поляризации может быть как плоскость параллельная земной поверхности, так и перпендикулярная ей, то обычно их называют соответственно горизонтальной и вертикальной плоскостью поляризации. Так, телевещание обычно производится в горизонтальной плоскости поляризации, а радиовещание − в вертикальной, хотя бывают и исключения.

Суперпозиция двух линейно поляризованных волн

Предположим теперь, что волна создается более сложной излучающей структурой и вектор имеет две составляющиеи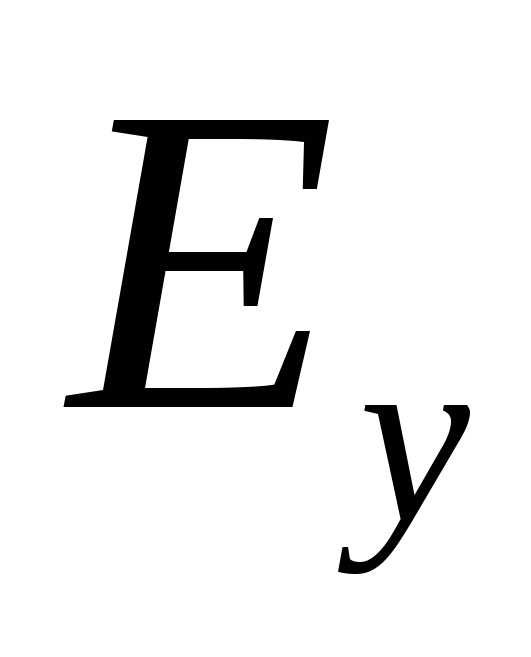, которые изменяются либо синфазно, либо с некоторым фазовым сдвигом. Векторв этом случае тоже имеет две составляющиеи, связанные с компонентами. Тогда в общем случае выражение для вектораплоской волны в среде без потерь записывается в виде

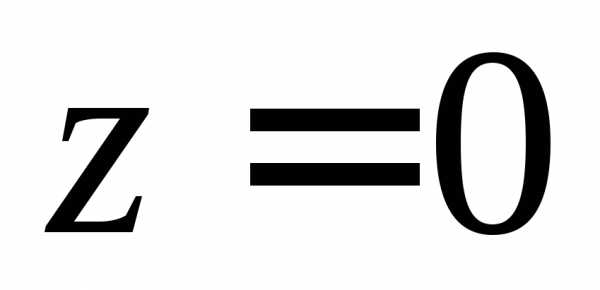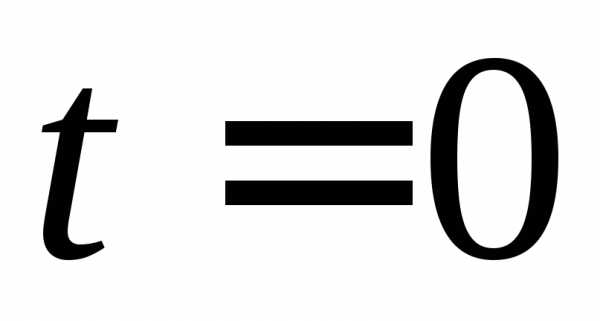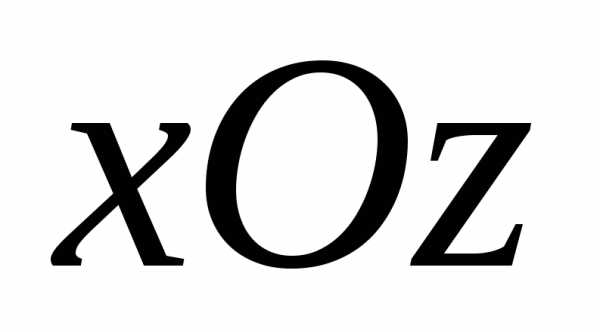где и− амплитуды составляющихисоответственно, аи− фазы этих составляющих в точкепри. Волну такого типа можно рассматривать как суперпозицию двух плоских линейно поляризованных волн со взаимно перпендикулярными плоскостями поляризациии, распространяющихся в одном направлении вдоль оси. Характер изменения векторас течением времени в фиксированной точке пространства зависит от соотношения между начальными фазами,и от амплитуд,.

Рассмотрим, что произойдет при отдельных частных случаях такой волны. Для этого рассмотрим угол между осью и векторомв некоторой фиксированной точке пространства. Очевидно, что величина этого угла зависит от соотношения между мгновенными значениями компонент вектора(рисунок Рисунок 52 ):

то есть, зависит от соотношения величин,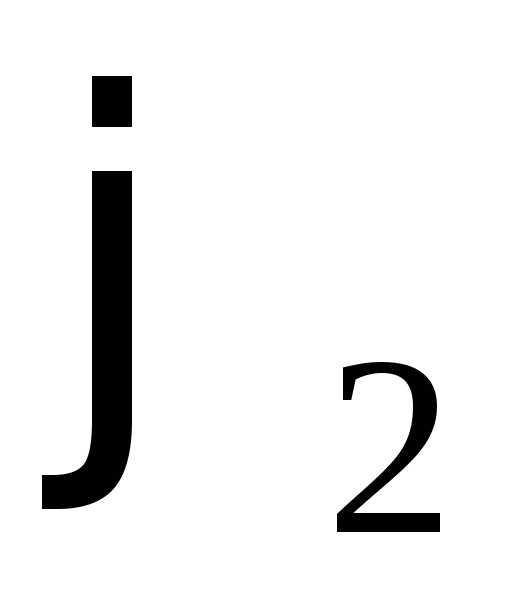и,и в общем случае меняется со временем. Для получения случая линейной поляризации необходимо, чтобы составляющие векторабыли синфазными или противофазными. Положим сначала, тогда

В этом случае вектор в любой момент времени лежит в плоскости, проходящей через осьи составляющей уголс плоскостью.

−Линейно поляризованная волна

Аналогичное явление имеет место также в том случае, когда разность между начальными фазами равна целому числу :

, где

Очевидно, что при 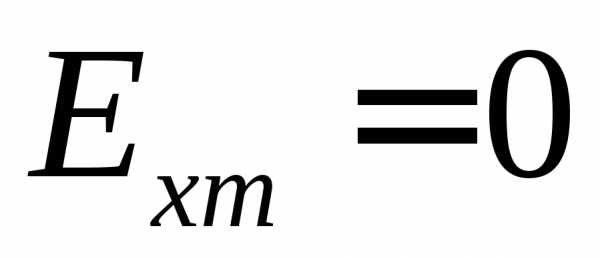илилинейно поляризованная волна превращается в волну с чисто горизонтальной или чисто вертикальной поляризацией.

− Горизонтальная и вертикальная поляризация

Рассмотрим второй частный случай. Пусть амплитуды составляющих иравны, а начальные фазы отличаются на:

Тогда

Подставляя эти значения в выражение для угла , получим:

откуда следует, что

где − целое число. Это равенство означает, что уголв фиксированной точке пространства

Таким образом, в фиксированной точке пространства вектор , оставаясь неизменным по величине, вращается с угловой частотойвокруг направления оси. Конец вектора при этом описывает окружность (рисунок Рисунок 54 ). Волны такого типа называются волнами с круговой поляризацией.

−Круговая поляризация плоской волны

Нетрудно убедиться также, что волна будет иметь круговую поляризацию не только в случае , но и

где .

Вдоль направления распространения (вдоль оси

В зависимости от направления вращения вектора вокруг оси распространения различают волны с левой и правой круговой поляризацией. В случае правой поляризации вектор вращается по часовой стрелке, если смотреть вдоль направления распространения, а в случае левой круговой поляризации − против стрелки. В рассмотренном примере приволна имеет правую поляризацию. Очевидно, что такая же поляризация будет в случае

В случае

волна имеет левую круговую поляризацию.

Вектор однородной волны везде и в любой момент времени перпендикулярен векторуи пропорционален ему по величине. Таким образом, в отличие от линейной поляризации, поле бегущей волны с круговой поляризацией в любой момент времени ни в одной точке пространства не равно нулю.

В случае среды с потерями линия, соединяющая концы векторов в один м тот же момент времени в разных точках оси , представляет собой спираль с радиусом, который изменяется вдоль оси по закону.

В самом общем случае распространения волны, когда конец векторабудет описывать при фиксированном и переменномв пространстве некий эллипс (рисунок Рисунок 55 ). Полуоси эллипса в общем случае не совпадают с осями координат.

−Эллиптически поляризованная волна

Для определения эллиптичности поля используется коэффициент эллиптичности, характеризующий отношение малой полуоси эллипса к большой:

При эллипс вырождается в окружность, этот случай соответствует электромагнитной волне с круговой поляризацией. Если, то эллипс вырождается в прямую линию − это линейно поляризованная волна.

При рассмотрении эллиптической и круговой поляризаций нами рассматривалась суперпозиция двух линейно поляризованных волн. Как мы увидели, поле с любым типом поляризации можно представить суммой двух волн, поляризованных линейно в двух ортогональных плоскостях. Можно доказать и обратное: эллиптически или линейно поляризованную волну можно представить в виде суммы двух волн с круговой поляризацией и противоположными направлениями вращения.

studfiles.net

Поляризация волн — это… Что такое Поляризация волн?

Поляриза́ция волн — характеристика поперечных волн, описывающая поведение вектора колеблющейся величины в плоскости, перпендикулярной направлению распространения волны.

В продольной волне поляризация возникнуть не может, так как направление колебаний в этом типе волн всегда совпадают с направлением распространения.^[1]

Причиной возникновения поляризации волн может быть:

несимметричная генерация волн в источнике возмущения;
анизотропность среды распространения волн;
преломление и отражение на границе двух сред.

Основными являются два вида поляризации:

линейная — колебания возмущения происходят в какой-то одной плоскости. В таком случае говорят о «плоско-поляризованной волне»;
круговая — конец вектора амплитуды описывает окружность в плоскости колебаний. В зависимости от направления вращения вектора может быть правой или левой.

Поляризация описывается Фигурами Лиссажу и соответствует сложению поперечных колебаний равной частоты.

Линейная поляризация
Круговая поляризация
Эллиптическая поляризация

Поляризация электромагнитных волн

Для электромагнитных волн поляризация — явление направленного колебания векторов напряженности электрического поля E или напряженности магнитного поля H.

Теория явления

Электромагнитная волна может быть разложена (как теоретически, так и практически) на две поляризованные составляющие, например, поляризованные вертикально и горизонтально. Возможны другие разложения, например, по иной паре взаимно перпендикулярных направлений, или же на две составляющие, имеющие левую и правую круговую поляризацию. При попытке разложить линейно поляризованную волну по круговым поляризациям (или наоборот) возникнут две составляющие половинной интенсивности.

Линейную поляризацию имеет обычно излучение антенн.

Если рассеянный свет поляризовать, то, используя поляризационный фильтр с иной поляризацией, можно ограничивать прохождение света. Интенсивность света, прошедшего через поляризаторы, подчиняется закону Малюса. На этом принципе работают жидкокристаллические экраны.

Некоторые живые существа^[2], например пчёлы, способны различать линейную поляризацию света, что даёт им дополнительные возможности для ориентации в пространстве. Обнаружено, что некоторые животные, например креветка-богомол павлиновая^[3] способны различать циркулярно-поляризованный свет, то есть свет с круговой поляризацией.

История открытия поляризации электромагнитных волн

В своих опытах Гюйгенс пошёл дальше Бартолина, пропуская оба луча, вышедшие из кристалла исландского шпата, сквозь второй такой же кристалл. Оказалось, что если оптические оси обоих кристаллов параллельны, то дальнейшего разложения этих лучей уже не происходит. Если же второй ромбоэдр повернуть на 180 градусов вокруг направления распространения обыкновенного луча, то при прохождении через второй кристалл необыкновенный луч претерпевает сдвиг в направлении, противоположном сдвигу в первом кристалле, и из такой системы оба луча выйдут соединёнными в один пучок. Выяснилось также, что в зависимости от величины угла между оптическими осями кристаллов изменяется интенсивность обыкновенного и необыкновенного лучей.

Параметры Стокса

В общем случае плоская монохроматическая волна имеет правую или левую эллиптическую поляризацию. Полная характеристика эллипса даётся тремя параметрами, например, полудлинами сторон прямоугольника, в который вписан эллипс поляризации , и разностью фаз , либо полуосями эллипса , и углом между осью и большой осью эллипса. Удобно описывать эллиптически поляризованную волну на основе параметров Стокса:

Независимыми являются только три из них, ибо справедливо тождество:

Если ввести вспомогательный угол , определяемый выражением (знак соответствует левой, а — правой поляризации^[4]), то можно получить следующие выражения для параметров Стокса:

На основе этих формул можно характеризовать поляризацию световой волны наглядным геометрическим способом. При этом параметры Стокса , , интерпретируются, как декартовы координаты точки, лежащей на поверхности сферы радиуса . Углы и имеют смысл сферических угловых координат этой точки. Такое геометрическое представление предложил Пуанкаре ^{[уточнить]}, поэтому эта сфера называется сферой Пуанкаре. В математике этой модели соответствует сфера Римана, в других разделах физики — сфера Блоха.

Наряду с , , используют также нормированные параметры Стокса , , . Для поляризованного света .

Практическое значение

Скорость распространения волны может зависеть от её поляризованности.

Две волны, линейно поляризованные под прямым углом друг к другу, не интерферируют.

Круговая поляризация применяется в антеннах космических линий связи, так как для приёма сигнала не важно положение плоскости поляризации передающей и приёмной антенн. То есть вращение космического аппарата не повлияет на возможность связи с ним. В наземных линиях используют антенны линейной поляризации — всегда можно выбрать заранее — горизонтально или вертикально располагать плоскость поляризации антенн. Антенну круговой поляризации выполнить сложнее, чем антенну линейной поляризации. Вообще, круговая поляризация — вещь теоретическая. На практике говорят об антеннах эллиптической поляризации — с левым или правым направлением вращения.

Круговая поляризация света используется также в технологиях стереокинематографа RealD и MasterImage. Эти технологии подобны IMAX с той разницей, что круговая поляризация вместо линейной позволяет сохранять стереоэффект и избегать двоения изображения при небольших боковых наклонах головы.

Поляризация частиц

В общем случае она имеет вид

Здесь — вектор, составленный из матриц Паули, а — вектор среднего спина частицы. Величина

называется степенью поляризации частицы. Это вещественное число Значение соответствует полностью поляризованному пучку частиц, при этом

где — вектор состояния частицы. Фактически, полностью поляризованные частицы можно полностью описать вектором состояния.

См. также

Примечания

↑ Волны — статья из Большой советской энциклопедии
↑ Некоторые люди также обладают способностью различать поляризацию света, в частности эти люди могут наблюдать невооруженным глазом эффекты, связанные с частичной поляризацией света дневного неба. Так описывает этот эффект Лев Николаевич Толстой в своей повести «Юность»:
«и, вглядываясь в растворенную дверь балкона … , и в чистое небо, на котором, как смотришь пристально, вдруг показывается как будто пыльное желтоватое пятнышко и снова исчезает;»
↑ MEMBRANA | Мировые новости | Учёные открыли новую форму зрительного восприятия
↑ Ахманов С.А., Никитин С.Ю. Физическая оптика. — МГУ,Наука, 2004. — P. 654. стр. 36. Знак соответствует левому винту в пространстве, при этом во времени происходит вращение по часовой стрелке, если смотреть вдоль волны.

Литература

Физика. Большой энциклопедический словарь/Гл. ред. А. М. Прохоров. — 4-е изд. — М.: Большая Российская энциклопедия, 1999. — С. 87. ISBN 5-85270-306-0 (БРЭ)
Ахманов С. А., Никитин С. Ю. — Физическая оптика, 2 издание, M. — 2004.
Борн М., Вольф Э. — Основы оптики, 2 издание, исправленное, пер. с англ.,М. — 1973

Ссылки

dic.academic.ru

Поляризация электромагнитных волн — это… Что такое Поляризация электромагнитных волн?

Поляризация — для электромагнитных волн это явление направленного колебания векторов напряженности электрического поля E или напряженности магнитного поля H. Когерентное электромагнитное излучение может иметь:

Линейную поляризацию — в направлении, перпендикулярном направлению распространения волны;
Круговую поляризацию — правую либо левую, в зависимости от направления вращения вектора индукции;
Эллиптическую поляризацию — случай, промежуточный между круговой и линейными поляризациями.

Некогерентное излучение может быть не поляризованным, либо быть полностью или частично поляризованным.

При теоретическом рассмотрении поляризации волна полагается распространяющейся горизонтально. Тогда можно говорить о вертикальной и горизонтальной линейных поляризациях волны.

Линейная

Круговая

Эллиптическая

Теория явления

Линейную поляризацию имеет обычно излучение антенн.

Некоторые живые существа^[1], например пчёлы, способны различать линейную поляризацию света, что даёт им дополнительные возможности для ориентации в пространстве. Обнаружено, что некоторые животные, например креветка-богомол павлиновая^[2] способны различать циркулярно-поляризованный свет, то есть свет с круговой поляризацией.

История открытия

Параметры Стокса

В общем случае плоская монохроматическая волна имеет правую или левую эллиптическую поляризацию. Полная характеристика эллипса даётся тремя параметрами, например, полудлинами сторон прямоугольника, в который вписан эллипс поляризации A₁, A₂ и разностью фаз φ, либо полуосями эллипса a, b и углом ψ между осью x и большой осью эллипса. Удобно описывать эллиптически поляризованную волну на основе параметров Стокса:

, ,

, .

Независимыми являются только три из них, ибо справедливо тождество:

Если ввести вспомогательный угол χ , определяемый выражением (знак соответствует правой, а — левой поляризации), то можно получить следующие выражения для параметров Стокса:

На основе этих формул можно характеризовать поляризацию световой волны наглядным геометрическим способом. При этом параметры Стокса , , интерпретируются, как декартовы координаты точки, лежащей на поверхности сферы радиуса . Углы и имеют смысл сферических угловых координат этой точки. Такое геометрическое представление предложил Пуанкаре, поэтому эта сфера называется сферой Пуанкаре.

Наряду с , , используют также нормированные параметры Стокса , , . Для поляризованного света .

См. также

Литература

Ахманов С. А., Никитин С. Ю. — Физическая оптика, 2 издание, M. — 2004.
Борн М., Вольф Э. — Основы оптики, 2 издание, исправленное, пер. с англ.,М. — 1973

Примечания

↑ Некоторые люди также обладают способностью различать поляризаци света, в частности эти люди могут наблюдать невооруженным глазом эффекты, связанные с частичной поляризацией света дневного неба. Так описывает этот эффект Лев Николаевич Толстой в своей повести «Юность»:
«и, вглядываясь в растворенную дверь балкона … , и в чистое небо, на котором, как смотришь пристально, вдруг показывается как будто пыльное желтоватое пятнышко и снова исчезает;»
↑ http://www.membrana.ru/lenta/?8088

dic.academic.ru

Поляризация волн — Википедия

В продольной волне поляризация возникнуть не может, так как направление колебаний в волнах этого типа всегда совпадает с направлением распространения^[1].

Поперечная волна характеризуется двумя направлениями: волновым вектором и вектором амплитуды, всегда перпендикулярным к волновому вектору. Волновой вектор показывает направление распространения волны, а вектор поляризации представляет собой вектор напряженности электрического поля. Так что в трёхмерном пространстве имеется ещё одна степень свободы — вращение вокруг волнового вектора.

Причиной возникновения поляризации волн может быть:

несимметричная генерация волн в источнике возмущения;
анизотропность среды распространения волн;
преломление и отражение на границе двух сред.

Зависимость мгновенных потенциалов при круговой поляризации

В общем случае для гармонических волн конец вектора колеблющейся величины описывает в плоскости, поперечной направлению распространения волны, эллипс, и такая поляризация называется эллиптической. Важными частными случаями являются линейная поляризация, при которой колебания возмущения происходят в какой-то одной плоскости, в таком случае говорят о «плоско-поляризованной волне», и круговая или циркулярная поляризация, при которой конец вектора амплитуды описывает окружность в плоскости колебаний, круговая поляризация в зависимости от направления вращения вектора может быть правой или левой.

Поляризация описывается Фигурами Лиссажу и соответствует сложению поперечных колебаний равной частоты.

Линейная поляризация
Круговая поляризация
Эллиптическая поляризация

Поляризация электромагнитных волн[править]

Теория явления[править]

Линейную поляризацию имеет обычно излучение антенн.

Некоторые живые существа, например пчёлы, способны различать линейную поляризацию света, что даёт им дополнительные возможности для ориентации в пространстве. Обнаружено, что некоторые животные, например креветка-богомол павлиновая^[2] способны различать циркулярно-поляризованный свет, то есть свет с круговой поляризацией. Некоторые люди также обладают способностью различать поляризацию света, в частности, эти люди могут наблюдать невооруженным глазом эффекты, связанные с частичной поляризацией света дневного неба. Так описывает этот эффект Лев Николаевич Толстой в своей повести «Юность»: «и, вглядываясь в растворенную дверь балкона … , и в чистое небо, на котором, как смотришь пристально, вдруг показывается как будто пыльное желтоватое пятнышко и снова исчезает;»

История открытия поляризации электромагнитных волн[править]

В 1810 году Малюс открыл закон, выражающий зависимость интенсивности линейно-поляризованного света после его прохождения через поляризатор от угла между плоскостями поляризации падающего света и поляризатора. В том же году он создал количественную корпускулярную теорию поляризации света, объяснившую все известные к тому времени поляризационные явления: двойное лучепреломление света в кристаллах, закон Малюса, поляризацию при отражении и преломлении. Несколькими годами позже Био открыл вращение плоскости поляризации, которое сам же и объяснил на основе теории Малюса.

Явление поляризации считалось доказательством корпускулярной теории света и опровержением волновой теории. Но в 1815 году Ампер сказал Френелю, что поляризацию можно объяснить, предположив, что эфир совершает поперечные колебания. В 1817 году ту же гипотезу выдвинул Юнг. В 1821 году Френель создал волновую теорию поляризации света.

Поляризация монохроматических волн[править]

В случае плоской монохроматической волны компоненты вектора напряженности электрического поля (также как и компоненты вектора напряженности магнитного поля) меняются совместно по гармоническому закону:

Здесь набег фазы .

Преобразовав и сложив первые два уравнения, можно получить уравнение движения вектора :

, где разность фаз .

Эта квадратичная форма описывает эллипс. То есть конец вектора напряженности плоской монохроматической волны описывает эллипс. Для того, чтобы привести её к каноническому виду, нужно повернуть эллипс на угол :

Любой эллипс можно задать в параметрической форме:

Здесь и — амплитудные значения компонент вектора , соответствующие большой и малой полуосям эллипса. Из последних двух систем уравнений можно сделать следующий вывод:

где — вектор Пойнтинга. Таким образом, в плоской монохроматической волне величина вектора Пойнтинга равна сумме потоков в двух произвольных ортогональных направлениях. Вводя обозначения и , из тех же двух систем уравнений можно вывести соотношения:

.^[3]

С помощью последних трех уравнений можно вычислить все параметры эллиптически поляризованной волны. А именно, зная величины и в произвольной системе координат, можно вычислить величину вектора Пойнтинга. С помощью разности фаз можно определить угол поворота большой оси эллипса относительно нашей системы координат, а также величины большой и малой полуосей эллипса и .

Направление вращения волнового вектора определяется разностью фаз . Если , тогда поляризация называется правой, а если, напротив, , поляризация называется левой. Если наблюдатель смотрит навстречу световому лучу, то правой поляризации соответствует движение конца вектора по часовой стрелке, а левой поляризации — против часовой стрелки. Если разность фаз равна , где — целое число, то эллипс вырождается в отрезок. Такая поляризация называется линейной. Другой важный случай возникает, когда и . В этом случае эллипс превращается в окружность, параметрическое уравнение которой имеет вид:

Нетрудно убедиться, что произвольная эллиптическая поляризация может быть разложена на сумму правой и левой круговых поляризаций.

Параметры Стокса[править]

Для описания поляризации плоской монохроматической волны достаточно трёх параметров, например полудлин сторон прямоугольника, в который вписан эллипс поляризации , и разностью фаз , либо полуосей эллипса , и углa между осью и большой осью эллипса. Стоксом было предложено альтернативное описание поляризации с помощью четырёх параметров, получивших его имя.

Независимыми являются только три из них, ибо справедливо тождество:

Используя вспомогательный угол , определяемый выражением (знак соответствует левой, а — правой поляризации^[4]), то можно получить следующие выражения для параметров Стокса:

Наряду с , , используют также нормированные параметры Стокса , , . Для поляризованного света .

s— и p-поляризации волн[править]

Подробнее смотрите Формулы Френеля.

В оптике и электродинамике s-поляризованная волна (сравните нем. senkrecht — перпендикулярный) имеет вектор электрического поля E, перпендикулярный плоскости падения. s-поляризованную волну также называют σ-поляризованной, сагиттально поляризованной, волной E-типа^[5], TE-волной (Transverse Electric)^[6]. p-поляризованная волна (сравните лат. parallel — параллельный) имеет вектор электрического поля E, параллельный плоскости падения. p-поляризованную волну также называют π-поляризованной, поляризованной в плоскости падения, волной H-типа^[5], TM-волной (Transverse Magnetic)^[6].

Термины TM-волна и TE-волна в работах ряда авторов^[7]^[8] меняются местами. Дело в том, что классически плоская граница предполагает однородность структуры в двух направлениях. В этом случае определяют плоскость падения и перпендикулярность напряженностей по отношению к ней. Разделение электромагнитного поля на два несвязанных решения возможно в более общем случае структуры, однородной в одном направлении. В этом случае удобно определять перпендикулярность напряжённостей по отношению к направлению однородности^[7]. Распространение последнего определения на частный классический случай приводит к тому, что напряженность, перпендикулярная к направлению однородности, оказывается в плоскости падения. Отмечается, что в случае металлической поверхности существенны только волны с электрической напряженностью, перпендикулярной к границе металла^[7]. Такие волны также удобнее называть TE-волнами. Термины TM и TE связаны также с обозначением поперечных мод в лазерном резонаторе или волноводе.

В сейсмологии p-волна (от англ. primary — первичный) — продольная волна, приходящая от эпицентра землетрясения первой. s-волна (от англ. secondary — вторичный) — поперечная волна (shear wave), имеющая меньшую скорость распространения, чем продольная, и поэтому приходящая от эпицентра позднее.

Практическое значение[править]

Скорость распространения волны может зависеть от её поляризации.

Две волны, линейно поляризованные под прямым углом друг к другу, не интерферируют.

Круговая поляризация применяется в антеннах космических линий связи, так как для приёма сигнала не важно положение плоскости поляризации передающей и приёмной антенн. То есть вращение космического аппарата не повлияет на возможность связи с ним. В наземных линиях используют антенны линейной поляризации — всегда можно выбрать заранее — горизонтально или вертикально располагать плоскость поляризации антенн. Антенну круговой поляризации выполнить сложнее, чем антенну линейной поляризации. Вообще, круговая поляризация — вещь теоретическая. На практике говорят об антеннах эллиптической поляризации — с левым или правым направлением вращения.

Поляризация частиц[править]

В общем случае она имеет вид

Здесь — вектор, составленный из матриц Паули, а — вектор среднего спина частицы. Величина

↑ Волны — статья из Большой советской энциклопедии.
↑ MEMBRANA | Мировые новости | Учёные открыли новую форму зрительного восприятия
↑ H. G. Jerrapd (1954). «Transmission of Light through Birefringent and Optically Active Media: the Poincare Sphere». JOSA 44 (8): 634-640.
↑ Ахманов С.А., Никитин С.Ю. Физическая оптика. — МГУ,Наука, 2004. — P. 654. стр. 36. Знак соответствует левому винту в пространстве, при этом во времени происходит вращение по часовой стрелке, если смотреть вдоль волны.
↑ ^5,0^5,1 Борн 1973, С. 77
↑ ^6,0^6,1 Фейнман 1965, 24.7
↑ ^7,0^7,1^7,2 Allen Taflove and Susan C. Hagness. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.. — Artech House Publishers, 2005. — ISBN 1-58053-832-0. Section 3.3, Reduction to two dimentions. p. 54-56
↑ Jean-Michel Lourtioz, Henri Benisty, Vincent Berger, Jean-Michel Gerard, Daniel Maystre, Alexei Tchelnokov Photonic crystals: towards nanoscale photonic devices. Springer. Berlin. 2008. Section 2.1.1, p.67 (ISBN 978-3-540-78346-6)

Физика. Большой энциклопедический словарь/Главный редактор А. М. Прохоров. — 4-е издание — М.: Большая Российская энциклопедия, 1999. — С. 87. ISBN 5-85270-306-0 (БРЭ)
Ахманов С. А., Никитин С. Ю. — Физическая оптика, 2 издание, M. — 2004.
Борн, М. & Э. Вольф. (1973), written at М., Основы оптики, пер. с англ. (2, исправленное ed.), Наука
Фейнман, Р. & Лейтон Р., Сэндс М. (1965), written at М., Фейнмановские лекции по физике. Том 6: Электродинамика. Перевод с английского (3 ed.), Эдиториал УРСС, 2004, ISBN 5-354-00704-6

ref>Некоторые люди также обладают способностью различать поляризацию света, в частности эти люди могут наблюдать невооруженным глазом эффекты, связанные с частичной поляризацией света дневного неба. Так описывает этот эффект Лев Николаевич Толстой в своей повести «Юность»:

www.wikiznanie.ru

1.3. Поляризация электромагнитных волн | Политех в Сети

Выше на основе уравнений Максвелла было показано, что в бегущей плоской электромагнитной волне векторы и в каждой точке и в каждый момент времени образуют с волновым вектором правую тройку векторов. В этом заключается свойство поперечности электромагнитных волн.

Выберем ось OZ системы координат вдоль волнового вектора . Тогда у векторов и могут быть отличны от нуля только проекции на оси OX и OY . Уравнения Максвелла допускают, в частности, такое решение, когда у вектора во всех точках и во все моменты времени отлична от нуля только одна проекция, например EX(Z,T). Вследствие упомянутого выше свойства поперечности, у вектора будет отлична от нуля только проекция на ось Y, т. е. By(Z,T). Мгновенный «снимок» такой волны, показывающий векторы и в разных точках оси Z в один момент времени приведен на рис. 1.7.

Р и с. 1.7

В таком случае говорят, что волна имеет линейную, или плоскую, поляризацию. В плоскости, перпендикулярной направлению распространения, концы векторов и за период описывают две взаимно перпендикулярные линии, длина которых определяется удвоенной амплитудой соответственно электрической и магнитной составляющих поля. Плоскость, в которой лежит вектор напряженности электрического поля волны и волновой вектор , называют Плоскостью Поляризации или плоскостью колебаний. Чтобы представить себе изменения электрического и магнитного полей с течением времени, можно считать, что вся система векторов на рис. 1.7 движется как целое вдоль оси Z со скоростью C.

Эллиптическая поляризация

В рассмотренном примере линейно поляризованной волны предполагалось, что вектор во всех точках направлен параллельно или антипараллельно оси X (см. рис. 1.7). В общем случае у плоской гармонической волны, распространяющейся вдоль оси Z, отличны от нуля обе компоненты Ex и Ey, а вектор электрического поля имеет вид , где , – единичные векторы, направленные вдоль осей ОX, Oy декартовой системы координат.

Рассмотрим волну, компоненты электрического поля которой изменяются по гармоническому закону

, , где D — сдвиг фаз между колебаниями.

Найдем уравнение траектории, по которой движется конец вектора в плоскости Z = Const. Перепишем в виде и с помощью исключим из этого равенства cos (WT – Kz) и sin (WT – Kz):

Напомним, что амплитуды E10 И E20 предполагаются положительными числами. Перенесем первое слагаемое правой части на левую сторону, делим обе части на E20 и возводим их в квадрат.

Раскрываем скобки и приводим уравнение к виду

Соотношение является уравнением конического сечения. Сечение имеет форму эллипса, так как соответствующий детерминант неотрицателен, т. е.

Р и с. 1.8

Эллипс вписан в прямоугольник, стороны которого имеют длины 2E10 и 2E10 (рис. 1.8). Он касается сторон прямоугольника в точках AA¢ (±E10, ±E20cosD) и BB¢ (±E10cosD, ±E20).

Итак, в общем случае при распространении плоской монохроматической световой волны конец вектора в плоскости Z = const описывает эллипс. Аналогично ведет себя и вектор напряженности магнитного поля. Такая волна называется Эллиптически поляризованной.

Представить себе электрическое поле такой волны при фиксированном T можно так: на поверхности прямого эллиптического цилиндра проведена винтовая линия, начала всех векторов находятся в точках оси цилиндра, концы — на винтовой линии, причем сам вектор везде перпендикулярен оси.

Правая и левая эллиптические поляризации

Двигаясь по эллипсу в плоскости Z = const, конец вектора может вращаться по часовой или против часовой стрелки. Для того чтобы различить эти два состояния, в оптике вводят понятия Правой поляризации (для наблюдателя, смотрящего навстречу световому лучу, вращение происходит по часовой стрелке) и Левой поляризации (вращение вектора в противоположном направлении). Покажем, что направление вращения вектора зависит от знака разности фаз D. Выберем момент времени T0, для которого WT0 – Kz = 0. В этот момент, согласно формулам и, ,.Так что . Из формулы видно, что в тот момент, когда конец вектора достигает крайней правой точки своей траектории (рис. 1.8), имеем DEy/Dt < 0, если 0 < D < P, и DEy/Dt > 0, если – P < D < 0. Очевидно, что первый из этих случаев соответствует право поляризованной волне, а второй — лево поляризованной.

Итак, в общем случае плоская монохроматическая волна имеет правую или левую эллиптическую поляризацию. Полная характеристика эллипса поляризации дается тремя параметрами E10, E20 и D. И, как видно из рис. 1.8, оси эллипса могут быть не параллельны осям Ox И Oy. Однако если заданы E10, E20 и разность фаз D, относящиеся к произвольному положению осей, и если A (0 < A £ P/2) — угол, определяемый соотношением, то главные полуоси эллипса A И B и угол Y (0 < Y £ P/2), который большая ось образует с осью Ox, находятся из формул ,

Где C (-P/4 £ C £ P/4) – вспомогательный угол, определяющий форму и ориентацию эллипса колебаний, а именно: .

Численное значение tgC определяет величину отношения осей эллипса, а знак при C характеризует два варианта, которые можно использовать при описании эллипса. Из последней формулы видно, что при правой эллиптической поляризации, когда sin D > 0, то угол C меняется в пределах 0 < C £ P/4, что соответствует знаку «+» в формуле. Соответственно для левой поляризации — знак «–».

Параметры A, B и Y можно определить на опыте, а, зная эти величины, по формулам можно рассчитать амплитуды E10, E20 и разность фаз D.

Линейная и круговая поляризации

Наиболее важны два частных случая, когда эллипс поляризации вырождается либо в прямую, либо в окружность.

Согласно и эллипс переходит в прямую при .

Тогда , и мы говорим о Линейной поляризации.

На рис. 1.9, а показаны два возможных направления поляризации в плоско поляризованной волне, соответствующие D = 0 и D = P.

Р и с. 1.9

Другой важный случай — случай Круговой поляризации волны, когда эллипс вырождается в круг. Необходимое условие этого вырождения заключается в превращении описанного прямоугольника в квадрат, т. е. амплитуды двух взаимно перпендикулярных компонент электрического поля должны быть равными .

Кроме того, одна из компонент должна равняться нулю, когда другая достигает максимального значения. Отсюда следует, согласно (1.37) и (1.38), что

И уравнение переходит в уравнение окружности .

В случае Правой поляризации sin D > 0, так что

, , где .

В случае Левой поляризации sinD < 0, так что ,

, где .

Из формул и следует, что .

Это означает, что сумма право — и лево- поляризованных волн дает линейно поляризованную волну.

Если вместо вещественного представления воспользоваться комплексным, т. е. вместо косинусов в и использовать экспоненциальные функции и ,то .

Из этого отношения сразу же можно определить характер поляризации:

А) Линейная поляризация .

Б) Правая круговая поляризация электрической волны

, .

В) Левая круговая поляризация

, .

В более общем случае можно показать, что для правой эллиптической поляризации мнимая часть отношения Ey/Ex положительна, тогда как для левой эллиптической поляризации она отрицательна.

На рис. 1.9, б показана круговая поляризация, на рис. 1.9, в эллипсы поляризации при разных значениях D.

Параметры Стокса. Сфера Пуанкаре

Как уже отмечалось, для определения эллипса поляризации необходимы три независимые величины, например амплитуды E10, E20 и разность фаз D или малая и большая оси A, B и угол Y, характеризующий ориентацию эллипса. Для практических целей состояние поляризации удобно задавать некоторыми параметрами, обладающими одинаковой физической размерностью. Такие параметры были введены Стоксом, и для любой волны их можно определить из простых экспериментов.

Для плоской монохроматической волны параметрами Стокса служат четыре величины.

Лишь три из них независимы, так как справедливо тождество

Очевидно, что параметр S0 пропорционален интенсивности волны. Параметры S1, S2, S3 простым образом связаны с углом Y, характеризующим ориентацию эллипса, и углом C, характеризующим эллиптичность и направление вращения. Справедливы следующие соотношения:

Например, последнее из уравнений можно получить, используя ранее записанные соотношения:

,,,,

И тригонометрические формулы.

Следовательно, .

Выражения подсказывают простое геометрическое представление различных состояний поляризации: S1, S2, S3 можно рассматривать как декартовы координаты точки P на сфере S радиуса S0, причем 2C и 2Y являются сферическими угловыми координатами этой точки (рис. 1.10). Каждому возможному состоянию поляризации плоской монохроматической волны заданной интенсивности (S0 = Const) соответствует одна точка на сфере S, и наоборот.

Так как угол C (или sin(2C)) положителен или отрицателен в зависимости от того, имеем ли мы дело с правой или левой поляризацией, то из последнего уравнения соотношений следует, что правая поляризация представляется точками на S, лежащими выше экваториальной плоскости, а левая – точками на S, лежащими ниже этой плоскости.

Р и с. 1.10

Для линейно поляризованного света разность фаз равна нулю или целому, кратному P. Тогда, согласно последнему уравнению соотношений, параметр Стокса S3 равен нулю, так что линейная поляризация представляется точками на экваториальной плоскости.

Правая круговая поляризация представляется северным полюсом (E10 = E20 = E00, S1 = 0, D = P/2, S2 = 0, S3 = S0), а левая поляризация – южным полюсом (E10 = E20 = E00, S1 = 0, D = – P/2, S2 = 0, ). Такое геометрическое представление различных состояний поляризации точками на сфере было предложено Пуанкаре. Оно чрезвычайно полезно в кристаллооптике для определения влияния материальных сред на состояние поляризации проходящего через них света. Сфера S называется сферой Пуанкаре.

В плоской монохроматической волне напряженность электрического поля (а также и магнитного поля ) есть Регулярная Функция Координат И Времени. Такая волна называется полностью поляризованной или просто поляризованной. Мы дали исчерпывающее представление о состояниях поляризации такой волны. Показали, что в общем случае такая волна поляризована эллиптически, а характеристики эллипса поляризации определяются амплитудами и фазами ортогональных компонент светового поля Ex и Ey.

Изложенное показывает, что электромагнитная волна с любой поляризацией может быть представлена в виде суперпозиции двух линейно поляризованных волн, плоскости колебаний электрического вектора (плоскости поляризации) которых взаимно перпендикулярны. Поэтому можно сказать, что электромагнитные волны обладают двумя независимыми состояниями поляризации.

Как мы видели, решением уравнений Максвелла служит монохроматическая волна, и поэтому она обязательно должна быть поляризована (в общем случае эллиптически). Однако опыт показывает, что излучение всех реальных источников света (кроме лазерных) неполяризовано. Это объясняется тем, что нам одновременно приходится наблюдать излучение огромного числа атомов, посылающих различно поляризованный свет. Кроме того, в каждом акте излучения атом испускает свет с новым состоянием поляризации. Таким образом, обычно наблюдается множество всех возможных ориентаций векторов и и быстрая смена этих ориентаций, что и представляет собой Естественный свет.

Естественный свет есть совокупность световых волн со всеми возможными направлениями колебаний, быстро и беспорядочно сменяющими друг друга; т. е. характеризуется неупорядоченностью направлений колебаний, совокупность эта статистически симметрична относительно волновой нормали.

Существует понятие Частично поляризованного света. Он характеризуется тем, что одно из направлений колебаний оказывается преимущественным, но не исключительным. Волновая нормаль уже не является прямой, по отношению к которой направления колебаний электрического (магнитного) вектора статистически равновероятны в плоскости, нормальной к этой прямой. Частично поляризованный свет можно рассматривать как смесь естественного и поляризованного. Можно в этом случае ввести понятие степени поляризации:

Где и – средние значения квадратов двух взаимно перпендикулярных компонент напряженности электрического поля, выбранных в плоскости, перпендикулярной направлению распространения волны.

Если P = 0, то свет неполяризованный или естественный; если P = 100%, то поляризация света линейная.

На практике поляризованное излучение получают или от лазерных источников, механизм работы которых мы рассмотрим позже, или используют специальные приборы, называемые Поляризаторами. С их помощью можно не только поляризовать излучение, но и анализировать состояние поляризации.

Поляризация электромагнитных волн | Наука

Круговая поляризацияПравить

История открытия Править

Параметры Стокса Править

Использование явления поляризации светаПравить

Поляризация волн | Наука | FANDOM powered by Wikia

Практическое значение Править

Поляризация частиц Править

Поляризация электромагнитных волн

Линейная поляризация

Суперпозиция двух линейно поляризованных волн

Поляризация волн — это… Что такое Поляризация волн?

Поляризация электромагнитных волн

Теория явления

История открытия поляризации электромагнитных волн

Параметры Стокса

Практическое значение

Поляризация частиц

См. также

Примечания

Литература

Ссылки

Поляризация электромагнитных волн — это… Что такое Поляризация электромагнитных волн?

Теория явления

История открытия

Параметры Стокса

См. также

Литература

Примечания

Поляризация волн — Википедия

Поляризация электромагнитных волн[править]

Теория явления[править]

История открытия поляризации электромагнитных волн[править]

Поляризация монохроматических волн[править]

Параметры Стокса[править]

s— и p-поляризации волн[править]

Практическое значение[править]

Поляризация частиц[править]

1.3. Поляризация электромагнитных волн | Политех в Сети

Добавить комментарий Отменить ответ